성냥개비가 불 댕긴 ‘3인 3색’ 수학 문제
수학개념 쏙쏙
저녁시간, 두 자매가 책상에 앉아 엄마와 수학 공부를 하고 있었다. 이제 막 구구단을 외우기 시작한 아현이는 교과서에 있는 문장제 문제를 풀다가 고개를 갸우뚱거리며 엄마에게 말했다.
“엄마, 이 문제는 어떻게 푸는 거에요?”
“성냥개비 3개로 삼각형 한 개를 만들었습니다. 삼각형 8개를 만들려면 성냥개비가 몇 개 필요합니까? 아현아, 이건 곱셈으로 푸는 거야.”
엄마는 문제를 읽어 주며 어떻게 푸는지 직접 일러 주었다. 하지만 아현이는 여전히 어쩔 줄 모르고 가만히 있었다. 답답한 마음에 ‘3곱하기 8을 하면 되잖아’라고 말해주고 싶었지만 꾹 참은 엄마는, 3학년인 큰 아이에게 설명을 해보라고 하는 것이 좋겠다는 생각이 들었다.
“서현아, 성냥개비 3개로 삼각형을 하나 만들면 삼각형 8개를 만들 때는 성냥개비가 몇 개 필요한지 알려면 어떻게 해야 하는지, 네 동생에게 설명 좀 해 줄래?”
마침 성냥개비 문제를 풀고 있던 서현이는, “그림을 그려 봐, 그러면 얼마나 쉬운데!”하며 그림을 그려 보였다.
<서현이가 그린 그림>
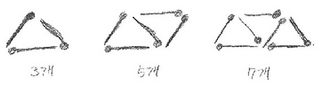 “자, 여길 봐. 맨 처음에 삼각형 한 개를 만들 때는 성냥개비 3개가 필요하지만 그 다음부터는 2개씩 늘어나지? 그러니까 3, 5, 7…. 이렇게 계속 2씩 더하면 돼. 그래서 답은 17개야!”
언니가 설명하는 사이, 아현이도 자신이 생각한 8개의 삼각형 그림을 그렸다.
<아현이가 그린 그림>
“자, 여길 봐. 맨 처음에 삼각형 한 개를 만들 때는 성냥개비 3개가 필요하지만 그 다음부터는 2개씩 늘어나지? 그러니까 3, 5, 7…. 이렇게 계속 2씩 더하면 돼. 그래서 답은 17개야!”
언니가 설명하는 사이, 아현이도 자신이 생각한 8개의 삼각형 그림을 그렸다.
<아현이가 그린 그림>
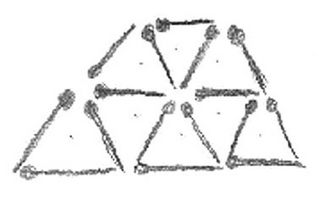 “근데 언니, 이렇게 그리면, 하나, 둘, 셋, 넷…열 여섯. 성냥개비는 모두 16개인데?”
두 아이가 서로 다른 답을 구한 것을 본 엄마는 답지에서 정답을 확인한 다음 아이들에게 말했다.
“물론 너희 둘의 주장이 맞고 그림도 다 맞는데, 정답은 아니구나. 아현이가 물어 본 문제는 2학년 곱셈 단원에 있는 문제였단다. 그러니까 3곱하기 8을 해야지.”
자매는 자신들이 왜 틀렸는지 모르겠다는 듯 어깨를 으쓱이며 서로를 쳐다보았다.
이 문제를 처음 읽었을 때, 세 사람의 머릿 속에 떠오른 그림은 서로 달랐다. 아현이는 얼마 전 언니와 비슷한 성냥개비 퍼즐 문제를 풀었던 것이 떠올랐다. 8개의 삼각형 모양이 머릿속에 대충 그려졌지만, 암산으로 성냥개비 수를 세기는 힘들어서 그냥 가만히 있었던 것이다. 엄마의 머리 속에 그려진 것은 각각 따로 떨어져 있는 8개의 삼각형 그림이었다. 반면 언니인 서현이는 ‘규칙을 찾는 문제’라고 생각했다. 최근 옆으로 이어진 삼각형 그림에서 변의 개수와 관련한 규칙을 찾는 문제를 푼 기억이 생생했기 때문이다.
결과적으로 보았을 때, 이 문제는 엄마가 생각한 대로 단순한 곱셈 문제였다. 하지만 문장을 읽으며 떠올리는 이미지는 사람마다 다 다르다. 이처럼 문제와 관련된 어떤 이미지나 해결 전략은 각자의 경험과 관련해 선택된다. 한 문제에 대해 서로 다른 생각을 하는 여러 사람들의 생각을 들여다보는 것은 자신의 생각을 반성하고 폭을 넓히는 좋은 경험이 될 것이다. 이런 경험이 쌓이면 한 문제, 한 문제를 좀 더 깊고 다양하게 푸는 습관을 들일 수 있다. (초등 수학 교과서 3-나, 112쪽) 강미선/<개념잡는 초등 수학사전> 저자
“근데 언니, 이렇게 그리면, 하나, 둘, 셋, 넷…열 여섯. 성냥개비는 모두 16개인데?”
두 아이가 서로 다른 답을 구한 것을 본 엄마는 답지에서 정답을 확인한 다음 아이들에게 말했다.
“물론 너희 둘의 주장이 맞고 그림도 다 맞는데, 정답은 아니구나. 아현이가 물어 본 문제는 2학년 곱셈 단원에 있는 문제였단다. 그러니까 3곱하기 8을 해야지.”
자매는 자신들이 왜 틀렸는지 모르겠다는 듯 어깨를 으쓱이며 서로를 쳐다보았다.
이 문제를 처음 읽었을 때, 세 사람의 머릿 속에 떠오른 그림은 서로 달랐다. 아현이는 얼마 전 언니와 비슷한 성냥개비 퍼즐 문제를 풀었던 것이 떠올랐다. 8개의 삼각형 모양이 머릿속에 대충 그려졌지만, 암산으로 성냥개비 수를 세기는 힘들어서 그냥 가만히 있었던 것이다. 엄마의 머리 속에 그려진 것은 각각 따로 떨어져 있는 8개의 삼각형 그림이었다. 반면 언니인 서현이는 ‘규칙을 찾는 문제’라고 생각했다. 최근 옆으로 이어진 삼각형 그림에서 변의 개수와 관련한 규칙을 찾는 문제를 푼 기억이 생생했기 때문이다.
결과적으로 보았을 때, 이 문제는 엄마가 생각한 대로 단순한 곱셈 문제였다. 하지만 문장을 읽으며 떠올리는 이미지는 사람마다 다 다르다. 이처럼 문제와 관련된 어떤 이미지나 해결 전략은 각자의 경험과 관련해 선택된다. 한 문제에 대해 서로 다른 생각을 하는 여러 사람들의 생각을 들여다보는 것은 자신의 생각을 반성하고 폭을 넓히는 좋은 경험이 될 것이다. 이런 경험이 쌓이면 한 문제, 한 문제를 좀 더 깊고 다양하게 푸는 습관을 들일 수 있다. (초등 수학 교과서 3-나, 112쪽) 강미선/<개념잡는 초등 수학사전> 저자
성냥개비가 불 댕긴 ‘3인 3색’ 수학 문제
성냥개비가 불 댕긴 ‘3인 3색’ 수학 문제
관련기사
항상 시민과 함께하겠습니다. 한겨레 구독신청 하기







![[사설] 노동자 안전 뒷전 중대재해법 후퇴가 민생 대책인가 [사설] 노동자 안전 뒷전 중대재해법 후퇴가 민생 대책인가](http://flexible.img.hani.co.kr/flexible/normal/300/180/imgdb/child/2024/0116/53_17053980971276_20240116503438.jpg)

![[올해의 책] 숙제를 풀 실마리를 찾아, 다시 책으로 ①국내서 [올해의 책] 숙제를 풀 실마리를 찾아, 다시 책으로 ①국내서](http://flexible.img.hani.co.kr/flexible/normal/800/320/imgdb/original/2023/1228/20231228503768.jpg)
![[올해의 책] 숙제를 풀 실마리를 찾아, 다시 책으로 ②번역서 [올해의 책] 숙제를 풀 실마리를 찾아, 다시 책으로 ②번역서](http://flexible.img.hani.co.kr/flexible/normal/500/300/imgdb/original/2023/1228/20231228503807.jpg)









